🔍 Web search with Google • Bing • DDG • Marginalia • Reddit • Spotify • Tootfinder • X • Yandex • Youtube • YTM
This you find in the 🏛️ Agora of Flancia
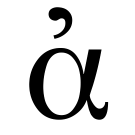
Loading Agora node...
🗣️ Stoas at [[20210116154952-category]]
A Stoa is a public space where people can meet and collaborate.
📖 Document at https://doc.anagora.org/20210116154952-category
📹 Meeting at https://meet.evolix.org/20210116154952-category
🤖 Agora AI assistant for [[20210116154952-category]]
Generative AI services provided by Mistral AI. To save a generation into the Agora, for now please copy/paste into a Stoa above.
🔎 Full text search for "20210116154952-category"
What could we show here?