📕 Node [[20210117123933 act4e_session_2_connection]]
📄 20210117123933-act4e_session_2_connection.md by @ryan
ACT4E - Session 2 - Connection
tags : [[category theory]]
source : ACT4E - Session 2 - Connection on Vimeo
Notes
-
Example: electrical distribution network
- Power plants -> high voltage nodes -> low voltage nodes -> consumers
- Can be represented as a directed graph
-
A set X to a set Y is a subset of \(X \times Y\) (cartesian product)
- Example: Given \(X = {x_1,x_2,x_3}, Y = {y_1,y_2,y_3,y_4}\), relation \(R \subseteq X \times Y\) is given by \(R = \{ \langle x_1,y_1 \rangle, \langle x_2,y_3 \rangle, \langle x_2,y_4 \rangle \}\)
- Note that this is not the whole cartesian product!
- We could write the above relation as \(X \xrightarrow{\text{R}} Y\), or \(R: X \to Y\)
- Relations are a type of morphism
-
Relations can be composed
- Given \(X \xrightarrow{\text{R}} Y\), \(Y \xrightarrow{\text{S}} Z\), we can compose the relation \(R \circ S\)
- \(R \circ S := \{\langle x, z \rangle \in X \times Z | \exists y \in Y: \langle x, y \rangle \in R \land \langle y, z \rangle \in S \}\) which is the relation \(X \to Z\)
-
The category Rel ([[Relation]]) of sets and relations:
- Objects: all sets
- Homsets: given sets X and Y: \(Hom_{Rel}(X,Y) := \mathcal{P}(X \times Y)\) = all subsets of \(X \times Y\)
- Identity morphisms
- Composition (above)
-
[[Functions are special types of relations]]
- \(R_f := \{\langle x,y \rangle \in X \times Y | y = f(x)\}\)
-
A function \(f: X \to Y\) is a relation \(R_f \subseteq X \times Y\) such that:
- \(\forall x \in X \exists y \in Y : \langle x,y \rangle \in R_f\) - every element of the source X gets mapped by f to some element of the target Y
- \(\exists \langle x_1,y_1 \rangle, \langle x_2,y_2 \rangle \in R_f\) holds: \(x_1 = x_2 \Rightarrow y_1 = y_2\)
-
Functions must therefore be defined everywhere
- For all values in X, there should be a corresponding Y value
- The opposite is not necessarily true
-
Lemma: Composition of relations generalizes the composition of functions
- \(X \xrightarrow{\text{f}} Y \xrightarrow{\text{g}} Z\) implies \(R_f \circ R_g = R_{f \circ g}\)
-
Properties of relations:
- Surjective: \(\forall y \in Y \exists x \in X : \langle x,y \rangle \in R\)
- Injective:
- Defined everywhere
- Single valued
-
Relations can be transposed
- \(R^T := \{\langle y,x \rangle \in Y \times X | \langle x,y \rangle \in R\}\)
- For \(R: X \to Y\), the transpose is \(R^T: Y \to X\)
- The transpose of the transpose of R is R
- The transpose relation holds all the same properties as the original relation
-
An [[Endorelation]] on set X is a relation \(X \to X\)
- Equality, for example, is an endorelation
- “Less than or equal” is also an endorelation
-
An endorelation is symmetric if:
- \(\forall x,x’ \in X: \langle x,x’ \rangle \in R \Leftrightarrow \langle x’,x \rangle \in R\)
- Example: x1 -> x2 and x2 -> x1
- Example: The relation “less than or equal” on all natural numbers is not symmetric
-
An endorelation is relfexive if:
- \(\forall x \in X : \langle x,x \rangle \in R\)
-
Example: less than or equal on all natural numbers in reflexive
- n <= n is reflexive
-
An endorelation is transitive if:
- \(\langle x,x’ \rangle \in R\) and \(\langle x’,x” \rangle \in R \Rightarrow \langle x,x” \rangle \in R\)
-
“Less than or equal” is transitive on all natural numbers
- l <= m and m <= n -> l <= n
- This property is reminiscent of composition in a category
-
An equivalence relation is an endorelation that is symmetric, relfexive, and transitive
- Notation: \(x \sim x’\) if \(\langle x,x’ \rangle \in R\)
- Partition of set X is a collection of subsets which are disjoint pairwise
- Category theory formalizes different notions and degrees of sameness
Backlinks
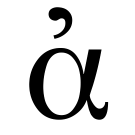
Rendering context...